Filosofia e arte em Poincaré

Poincaré teve grande contribuição na matemática, mas foi filósofo da ciencia, físico teórico, engenheiro e psicólogo, além do que suas fórmulas de equações tornaram-se verdadeiras obras de artes visuais.

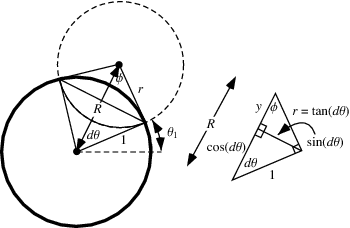
Em geometria, o modelo de disco Poincaré , também chamado o modelo de disco conformado é um modelo n -dimensional  de gemetria hiperbólica em que os pontos da geometria estão em um disco n -dimensional.

(...)
O eu inconsciente ou eu subliminar, como se costuma dizer, desempenha um papel essencial na criação matemática. Isto deduz-se de tudo o que atrás se disse.

Habitualmente considera-se o eu subliminar como puramente automático; ora bem, vimos que o trabalho matemático não é um simples trabalho mecânico que se poderia confiar a uma máquina por mais perfeita que a imaginassemos.

Não se trata apenas de aplicar regras e de elaborar o maior número possível de combinações através de leis fixas. As combinações assim obtidas seriam extremamente numerosas, inúteis e embaraçosas.

O verdadeiro trabalho do criador consiste em escolher entre estas combinações com o fim de eliminar as inúteis ou, sobretudo, nem sequer se dar ao trabalho de as realizar. As regras que conduzem a esta escolha são extremamente subtis e delicadas.

É quase impossível enunciá-las com uma linguagem precisa. É mais fácil senti-las do que formulá-las. Em tais condições como é possível imaginar um "crivo" capaz de as aplicar mecanicamente?

(...)Quais são os entes matemáticos a que atribuímos estas características de beleza e de elegância e que são susceptíveis de desencadear em nós um sentimento de emoção estética?

São aqueles cujos elementos estão dispostos harmoniosamente, de forma a que a mente possa sem esforço abraçar todo o conjunto penetrando em todos os seus detalhes.

Esta harmonia é simultaneamente uma satisfação para as nossas necessidades estéticas e um auxílio para a mente que a sustenta e guia. E, ao mesmo tempo, ao colocar perante os nossos olhos um conjunto bem ordenado, faz-nos pressentir uma lei matemática…

Assim, é esta sensibilidade estética especial que desempenha o papel do "crivo" delicado de que anteriormente falei. Isto permite compreender suficientemente porque é que quem a não possui não pode nunca vir a ser um verdadeiro criador.

(...)
A nossa escolha é livre para imaginar todas as convenções possíveis, mas, nessa escolha é guiada pelos factos experimentais.

"o sábio digno deste nome, o geómetra sobretudo, sente face à sua obra a mesma sensação que o artista; a sua felicidade revela-se da mesma grandeza e natureza. Se eu não escrevesse para um público apaixonado por ciência, não ousaria exprimir-me desta forma; temeria a incredulidade dos profanos. Mas aqui, posso exprimir todo o meu pensamento. Se trabalhamos, não é tanto no intuito de obter resultados positivos com os quais o homem vulgar pensa que estamos unicamente preocupados, é mais para sentir esta emoção estética e comunicá-la aos que são capazes de a entender."

A  lógica permite decompor cada demonstração num número muito grande de operações elementares. Mas, depois de examinarmos e constatarmos a correcção de cada uma dessas operações, teremos por isso compreendido o verdadeiro sentido da demonstração?