Geometria pura arte

A arte na geometria é uma área da filosofia da matemática que me fascina muito, tem tempos que ando batendo cabeça com esse assunto, desde que conheci a arte árabe, seus desenhos de arabescos nas mesquitas, ricos em geometria trdimensional, pensei: - mas como eles projetaram isso meldeus?  Então, cheguei nos estudos de "matemática no Islã medieval", esse livro é muito bom  "Geometria", em Roshdi Rashed, ed., Enciclopédia da História da Ciência Árabe , vol. 2,470p, Routledge , Londres e Nova York:, quase tudo na ciência foi motivado por fontes árabes pois eles traduziam tudo do mundo antigo, enquanto os cristãos queimavam tudo do mundo antigo.

"A hegemonia Árabe". pp 241-242. "Omar Khayyam (ca. 1050-1123) 

(...)Uma das contribuições mais frutíferas do ecletismo árabe foi a tendência para fechar a lacuna entre a álgebra numérica e geométrica. O passo decisivo nessa direção veio muito mais tarde com Descartes, mas Omar Khayyam estava se movendo nessa direção, quando escreveu: "Quem pensa que a álgebra é um truque na obtenção de incógnitas pensou em vão. Não deve ser dada atenção para o fato de que a álgebra e geometria são diferentes na aparência. "Álgebras são fatos geométricos que são comprovadas. "

Mulher no ensino da geometria . Ilustração no início de uma tradução medieval de Elementos de Euclides , (c.1310)

Na Idade Média , a matemática no Islã medieval contribuiu para o desenvolvimento da geometria, especialmente geometria algébricae álgebra geométrica.  Al-Mahani  concebeu a idéia de reduzir problemas geométricos, como duplicação do cubo para os problemas de álgebra. Thabit ibn Qurra (conhecido como Thebit em latim ) tratou de aritmética operações aplicadas a relações de quantidades geométricas, e contribuiu para o desenvolvimento da geometria analítica . Omar Khayyam (1048-1131) encontrou soluções geométricas para equações cúbicas . Os teoremas de Ibn al-Haytham (Alhazen), Omar Khayyam e Nasir al-Din al-Tusi emquadriláteros , incluindo o quadrilátero Lambert e quadrilátero Saccheri , foram cedo resultados em geometria hiperbólica e, junto com sua alternativa postula, como axioma de Playfair , estas obras tiveram uma influência considerável sobre o desenvolvimento da geometria não-euclidiana entre os geômetras tarde europeus, incluindo Witelo (c.1230-c.1314), Gersonides ( 1288-1344), Alfonso , John Wallis , e Giovanni Girolamo Saccheri .

Um europeu e um árabe a praticar geometria no século 15. 

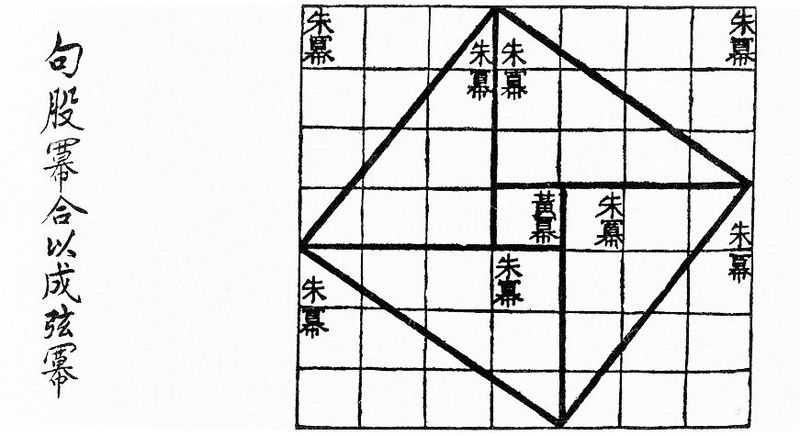
Pra quem gosta de geometria projetiva aplicada ao design, é o segredo dos artistas para quadros tão perfeitos tridimensional, bem representados num plano bidimensional

Geometria projetiva é uma geometria de medição ou sem linhas paralelas, apenas o estudo de como os pontos são relacionados uns com os outros.

Uma ilustração de teorema de Desargues " , um importante resultado em euclidiana e geometria projetiva . 

Geometria diferencial utiliza ferramentas de cálculo para estudar problemas de geometria. 

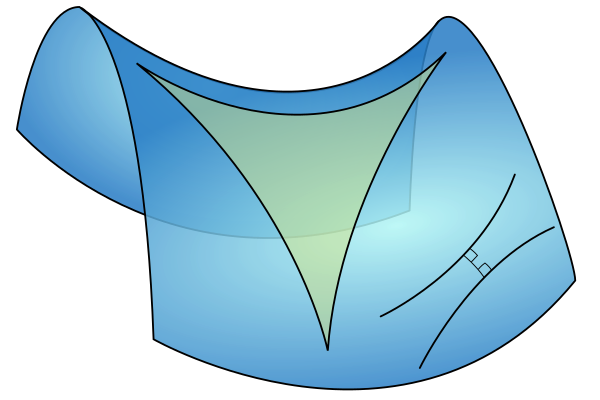
Mais sobre geometria